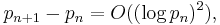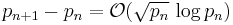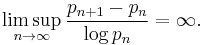Cramér's conjecture
In number theory, Cramér's conjecture, formulated by the Swedish mathematician Harald Cramér in 1936,[1] states that
where pn denotes the nth prime number, O is big O notation, and "log" is the natural logarithm. Intuitively, this means the gaps between consecutive primes are always small, and it quantifies asymptotically just how small they can be. This conjecture has not been proven or disproven.
Contents |
Heuristic justification
Cramér's conjecture is based on a probabilistic model (essentially a heuristic) of the primes, in which one assumes that the probability that a natural number x is prime is 1/log x. This is known as the Cramér model of the primes. Cramér proved that in this model, the above conjecture holds true with probability one.[1]
Proven results on prime gaps
Cramér also gave much weaker conditional proof that
on the assumption of the Riemann hypothesis.[1]
In the other direction, E. Westzynthius proved in 1931 that prime gaps grow more than logarithmically. That is,[2]
Cramér-Granville conjecture
Daniel Shanks conjectured asymptotic equality of record gaps, a somewhat stronger statement than Cramér's conjecture.[3]
In the random model,
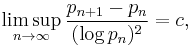 with
with 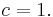
But this constant,  , may not apply to all the primes, by Maier's theorem. Andrew Granville in 1995 proposed the constant
, may not apply to all the primes, by Maier's theorem. Andrew Granville in 1995 proposed the constant 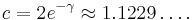 [4]
[4]
Thomas Nicely has calculated many large prime gaps.[5] He measures the quality of fit to Cramér's conjecture by measuring the ratio R of the logarithm of a prime to the square root of the gap; he writes, “For the largest known maximal gaps, R has remained near 1.13,” showing that, at least within the range of his calculation, the Granville refinement of Cramér's conjecture seems to be a good fit to the data.
See also
- Prime number theorem
- Legendre's conjecture and Andrica's conjecture, much weaker but still unproven upper bounds on prime gaps
References
- ^ a b c Cramér, Harald (1936), "On the order of magnitude of the difference between consecutive prime numbers", Acta Arithmetica 2: 23–46.
- ^ Westzynthius, E. (1931), "Über die Verteilung der Zahlen die zu den n ersten Primzahlen teilerfremd sind", Commentationes Physico-Mathematicae Helingsfors 5: 1–37.
- ^ Shanks, Daniel (1964), "On Maximal Gaps between Successive Primes", Mathematics of Computation (American Mathematical Society) 18 (88): 646–651, doi:10.2307/2002951, JSTOR 2002951.
- ^ Granville, A. (1995), "Harald Cramér and the distribution of prime numbers", Scandinavian Actuarial Journal 1: 12–28, http://www.dartmouth.edu/~chance/chance_news/for_chance_news/Riemann/cramer.pdf.
- ^ Nicely, Thomas R. (1999), "New maximal prime gaps and first occurrences", Mathematics of Computation 68 (227): 1311–1315, doi:10.1090/S0025-5718-99-01065-0, MR1627813, http://www.trnicely.net/gaps/gaps.html.